Perceptron Classifiers Written by Hand

perceptrons

A Python project implementing simple perceptron classifiers by hand

How to run

1. Download or clone the Git repository with git clone https://github.com/anjieyu/perceptrons.git
2. Navigate to the project directory with the command cd perceptrons
3. Run python3 main.py

What this project does

Data

The first thing this project does is load the training data from the data directory and store in a dictionary that maps all data points from each training data file and associates them with the file name that they came from.

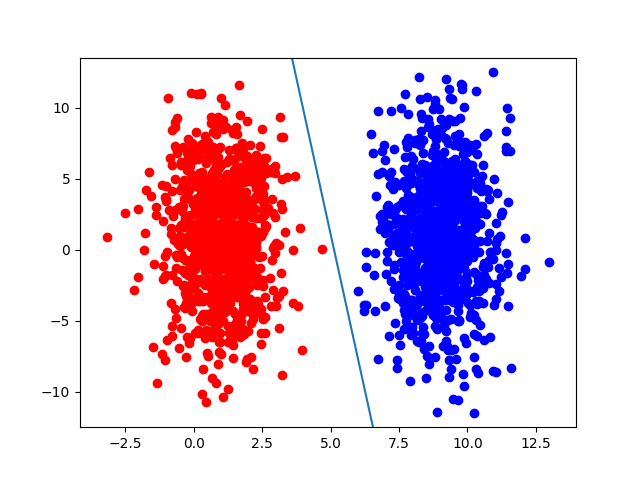
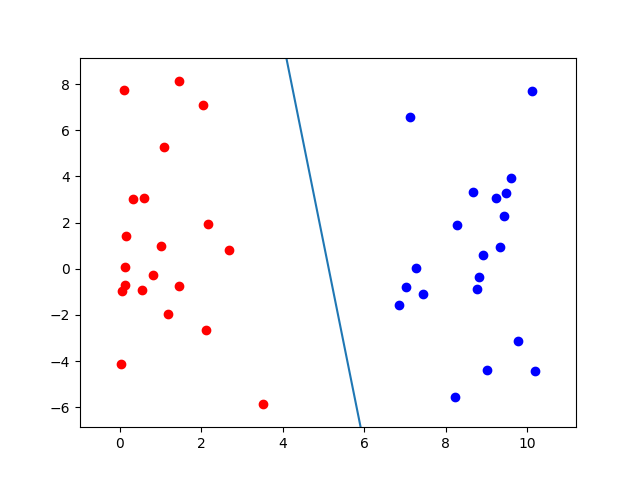
The dataset is a simple randomly generated dataset of 2 classes which are labeled 0 or 1 and consist of an x, y coordinate. Samples with an x value less than 5 are class 0. Samples with an x value greater than 5 are class 1. The samples are randomly generated from a Gaussian distribution. Each training dataset file has 100 samples. The test dataset has 2000 samples.

Perceptrons

After the data is imported, we create a perceptron for each training dataset. The perceptron class is located in the file perceptron.py and has a constructor and 3 methods.

• def __init__(self, inputs, classes):
  • The constructor takes in the number of features as inputs for each sample, and the number of classes for which to predict for.
  • To initialize a perceptron, this constructor also initializes weights based on the number of inputs from a range from 0 to 3.
  • A bias term is added with a constant feature input value of 1.5 and a randomized weight from 0 to 1.
  • Finally, a learning rate is set for the perceptron with a value of 0.85.
• def activate(self, sample):
  • The activation function takes the values of the sample as the input and multiplies each term with the corresponding weight for the feature. It also multiplies the bias term with the current bias weight and sums together the result of all features times their feature weights plus the bias times the bias weight.
  • The resulting value is the interpreted result of the sample by the perceptron given the perceptron’s current weights.
• def step(self, activation):
  • The step function is a simple step activation function that assigns a class to a sample if the activation is greater than 0. If the activation is greater than 0, the class is 1. If the activation is less than 0, then the class is 0.
• def learn(self, sample, label):
  • This function performs the weight updates for a perceptron after it receives a sample. It uses the activate and step functions to determine a class for a given sample.
  • If the predicted label does not match the actual label, then a weight update step will be performed on the perceptron, by adding or subtracting the current weight values times the sample features to the weights again.
  • The same is applied to the bias weight as well.
  • The learning rate is multiplied by the change in weight calculated from the previous step to normalize the weight update rule.
  • If the predicted label matches the actual label, then no weight update will be performed.

Each perceptron for each training set of data learns per sample, so the weight update rule is applied for each misclassification on a 1 to 1 basis. The decision boundary is updated for each misclassification per sample in each training set.

Evaluation

Since a perceptron is created for each training set, each trained perceptron is evaluated against a single holistic test dataset, for which there are 2000 samples. This means that 10 differently trained perceptrons are evaluated against the same 2000 test samples. Each perceptron consistently achieves 96% to 98% accuracy on the test data.

Graphing

In order to visualize the decision boundaries learned by each perceptron, the samples for the training and test datasets are graphed separately in 2 different matplotlib graph outputs. The decision boundary is calculated from the weights and the bias term learned by the perceptron from each training set. This boundary is graphed on each graph for each learned perceptron. These graphs usually show an angled boundary which is fitted to the training data, and is not perfectly aligned at x = 5. This is a good way to show how perceptrons generalize according to their training data, and try to learn or approximate functions from patterns in data.