Water Volume Game

By Anjie Yu With Instruction by Lauren Dennedy

May 2023 - August 2023

Introduction

The water volume game checks the volume of water that can be put between two pillars and compares it to see if the pair of pillars can store the most amount of water out of the nine randomized pillars. It is a 2D game made using the Unity Game Engine written with C#.

When the game starts, the nine pillars are randomized, and the player can choose two pillars. If they choose another pillar, then the older pillar that they chose will be replaced with the new pillar. When the player is satisfied with their choice, then they can click the submit button and the space between the two chosen pillars will be filled with water and the game will show them if they win or if they lose. The player wins if the two pillars that they chose can hold the most volume of water between their space. The game checks and compares all possible combinations of all pillars. If the player does not choose the two that hold the most volume of water, then they lose.

Even though this game is named the water volume game, the game is only two dimensional and thus the actual metric compared is surface area. This game is called the water volume game because it was based on a LeetCode problem referred to similarly. The way the water is drawn in the game looks like a reservoir of water that would be filled.

Test Cases

Test Case #1

Test to ensure that the player can win the game.

Scenario: the game starts normally with randomized pillars, where it is obvious which pillars satisfy the win condition.

Expected result: after selecting the two pillars and clicking submit, the player should win the game.

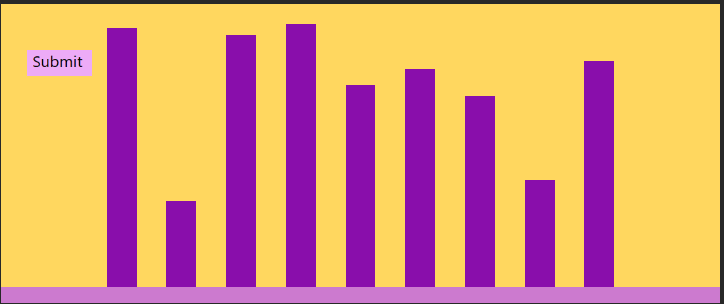
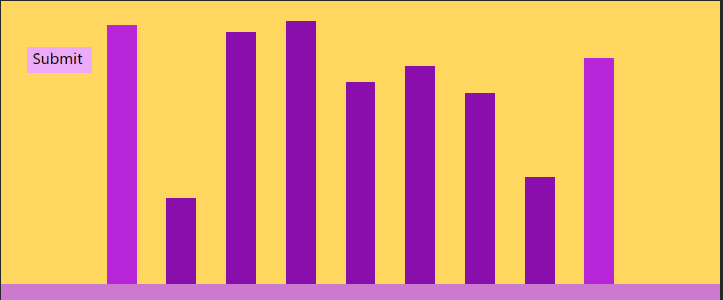
Actual result: The player wins in a case where the solution is obvious.

Test Case #2

Test to ensure that the player can lose the game.

Scenario: the game starts normally with randomized pillars, where it is obvious which pillars satisfy the win condition.

Expected result: after selecting the two pillars that would not win and clicking submit, the player should lose the game.

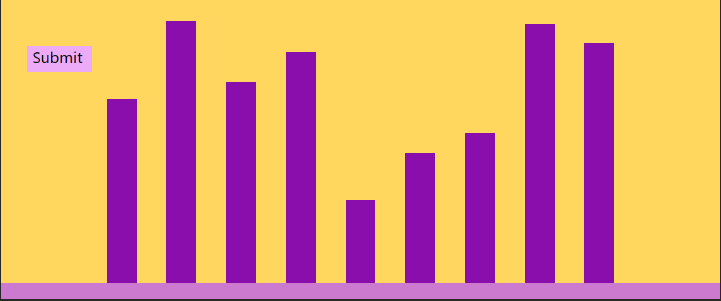
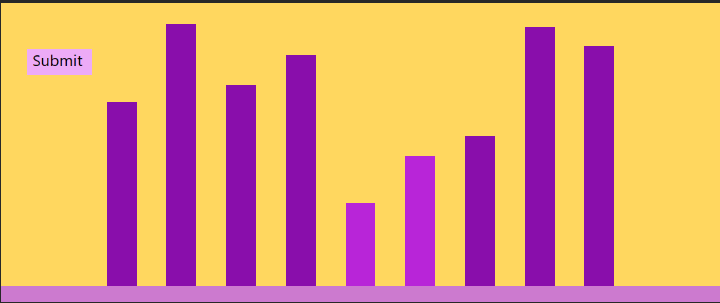
Actual result: 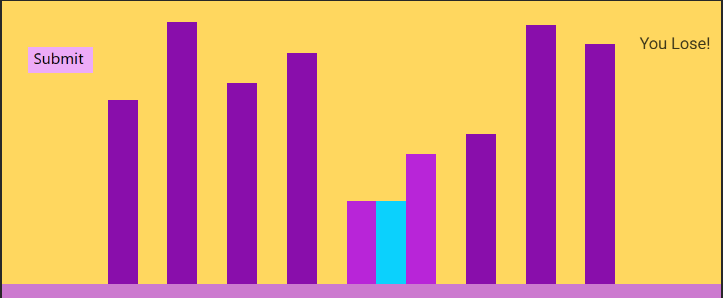The player loses the game.

Edge Cases

Edge Case #1

Scenario: what happens when the player presses submit with no pillars selected

Expected result: nothing should happen.

Actual result: nothing happens when the player presses submit.

Edge Case #2

Scenario: what happens when the player presses submit with one pillar selected

Expected result: nothing should happen.

Actual result: nothing happens when the player presses submit.

Edge Case #3

Scenario: what happens when the player presses submit for two pillars that have been selected after previously not having enough pillars selected (0 or 1)

Expected result: the game will successfully continue with the selected pillars and determine if the player wins or loses.

Actual result: the game continues successfully and determines a win or lose state for the player.

Edge Case #4

Scenario: what happens if the player tries to select more than two pillars

Expected result: the game only allows for two pillars selected at a time and when the player presses submit only the two most recent pillars will be used for the calculation for the water.

Actual result: only two pillars can be selected at a time.

Explanation of Data Structures and Algorithms for the Game

Pillars

• Each pillar was an instance of a pillar class that contained code to set a random height and offset its position according to the random height that was generated.
• The x position for each pillar is static. The height is dynamically generated and the y position is set accordingly. In order to accomplish this, we used the distance formula from the midpoint of the pillar to the bottom of the game.

Pillar Manager

• The pillar manager is a script used to control operations requiring all pillars at once. This includes:
• Algorithms to support the queue selector for the pillars
• Broadcast receivers and senders to draw water between the pillars
• Managing all “volumes” (surface area) between each possible pair of pillars.

Pillar Matrix

• The pillar matrix is a structure that was created specifically for the pillar manager to calculate all possible surface areas in the game and then determine which combination produces the largest value.
• The first step to creating the pillar matrix was to collect all of the pillars in order from left to right. Using the order of the pillars, we calculated the surface area of the shape drawn between the pillars constrained according to the smaller of the two pillars into a 2 dimensional matrix.
• What this means is that in the above positions, a float value is placed that represents the maximum surface area that can be drawn between the pillars in the specified positions. The positions 1x2, 1x3, for example, show that position representing the surface area between pillars 1 and 2, or 1 and 3, and so on.
• The inverted triangle shape is used because as you calculate each new row of pillars, certain combinations would have already been calculated in the previous rows. For example, in row 1, there is no 2x1 or 2x2 value because 2x1 is already represented by 1x2 in row 0 and there is no value for 2x2. Avoiding these redundant calculations creates this shape in the matrix.
• The surface area value, as mentioned before, is constrained by the minimum of the two pillars that are being calculated at each position. What this means, is that for example:
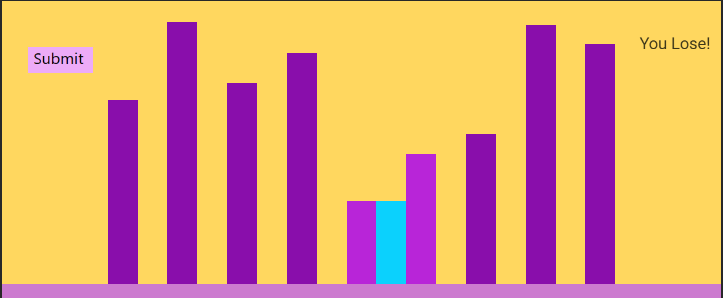
• In this picture, the water can only go up to the smaller pillar because in real life, the water would overflow past the smaller pillar if you tried to fill it up to the taller pillar.
• After all of the surface areas are calculated, with the knowledge of the row and column used at each position, the matrix can be used as a lookup table to find the two pillars that produce the maximum surface area in the whole game.
• Once the cell containing the maximum value has been found, the pillars that produce the value can be determined using the equations below:
• This works because the pillar surface areas were calculated based on the order of the pillars that had already been sorted from left to right. Without this presorting operation, the calculated values would have been completely irrelevant to their position in the matrix.
• Once the two pillars that produce the maximum surface area have been found, all that is left is to compare the best case pillars with the players chosen pillars. If the pairs match, the player wins.